在物理学的广阔天地中,球坐标系以其独特的魅力,成为描述空间中球对称问题的得力工具。张朝阳的物理课深入浅出地探讨了球坐标系下的体积微元,并巧妙地将其应用于验证均匀球体引力可等效到球心的经典问题。本文将跟随张朝阳的思路,一步步揭开球坐标系体积微元的神秘面纱,并探究均匀球体引力的等效性。
我们需要理解球坐标系的基本概念。与直角坐标系不同,球坐标系通过半径r、极角θ和方位角φ三个参数来描述空间中的点。这种坐标系特别适合处理球对称问题,因为它能够直接反映出物体的球对称性。
在球坐标系中,体积微元的推导是理解引力等效性的关键。体积微元dV可以表示为r^2sinθdrdθdφ,这一表达式揭示了球坐标系下体积的微观构成。通过积分,我们可以得到任意形状的体积。张朝阳在课程中详细讲解了这一推导过程,使学生们能够清晰地理解球坐标系下体积的计算方法。
我们将球坐标系的体积微元应用于均匀球体的引力计算。根据牛顿的万有引力定律,一个质量为m的质点受到一个质量为M的均匀球体的引力可以表示为F=GMm/r^2,其中G是引力常数,r是质点到球心的距离。然而,当我们考虑球体内部分布的质量时,问题就变得复杂起来。
张朝阳的物理课通过引入球坐标系,巧妙地将这一问题简化。他指出,对于均匀球体,可以将球体分割成无数个薄球壳,每个球壳对质点的引力可以等效地看作是集中在球心的一个质点。这一结论的证明依赖于球坐标系下体积微元的正确性。通过积分,我们可以计算出整个球体对质点的引力,并验证其等效性。
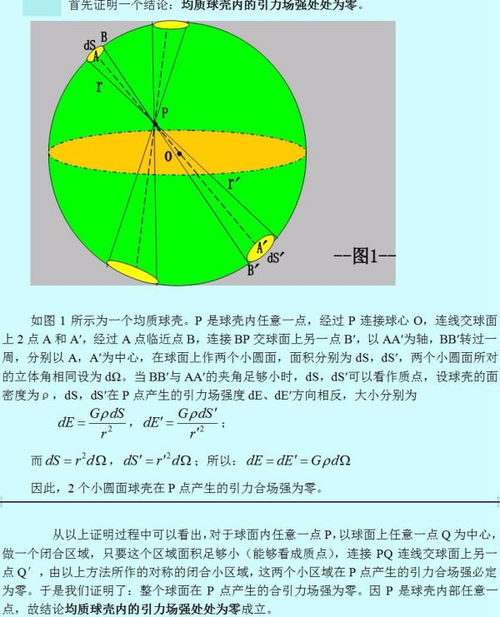
这一过程不仅展示了球坐标系在物理学中的强大威力,也体现了张朝阳物理课的深刻洞察力。他不仅教会学生如何使用数学工具解决物理问题,更重要的是,他教会学生如何思考,如何将复杂问题分解为可处理的部分,并逐一击破。
在文章的我们回顾了张朝阳物理课的核心内容,即球坐标系体积微元的推导和均匀球体引力的等效性验证。这两个看似独立的问题,在张朝阳的巧妙引导下,相互交织,共同揭示了物理学中的美妙和谐。通过这一课程,学生们不仅学到了知识,更学会了如何像物理学家一样思考问题,如何用数学语言描述自然界的规律。
《张朝阳的物理课》不仅是一堂物理课,更是一次思维的盛宴。它让我们看到了球坐标系的魅力,感受到了物理学的深邃,更重要的是,它激发了我们对知识的渴望和对探索的热情。在未来的学习和研究中,我们将带着张朝阳的教诲,继续在物理学的海洋中遨游,探索更多的未知领域。











评论